We are nearing the end of one of the main sections of this function series, but we have yet to look at one of the main elements you will see when using F#, which is signatures of functions.
In order to understand function signatures we will be revisiting our own old friend the “FSI Window”. We will start with some simple examples and then build up to more complex cases. So without further ado let’s begin.
The Basics
Unit : Unit is essentially void, and is expressed using the notation “()”
-> : Is the separator between the parameter, and the last arrow will point to the return value
Tuples : Are expressed using the familiar notation (x * y)
Functions : Are wrapped in “(..)” parentheses
Understanding Functions That Taken No Parameters
We will start with functions that take no parameters at all, and return values.
Returning A Int
let aSimpleIntegerFunction() = 12
Gives us this type definition
- aSimpleIntegerFunction : unit –> int
What that means is that the function takes unit (void) and returns an int
Returning A String
let aSimpleStringFunction() = "cat"
Gives us this type definition
- aSimpleStringFunction : unit -> string
What that means is that the function takes unit (void) and returns an string
Returning A Bool
let aSimpleBoolFunction() = true
Gives us this type definition
- aSimpleBoolFunction : unit -> bool
What that means is that the function takes unit (void) and returns an bool
Returning A Tuple
let aSimpleTupleFunction() = (1,"one")
Gives us this type definition
- aSimpleTupleFunction : unit -> int * string
What that means is that the function takes unit (void) and returns an tuple of int and string
Returning A Record
type SimplePerson = { Name : string; }
.....
let aSimpleRecordFunction() = { Name = "Alf" }
Gives us this type definition
- aSimpleRecordFunction : unit -> SimplePerson
What that means is that the function takes unit (void) and returns a SimplePerson record type
Returning A List
let aSimpleListFunction() = [1,2,3]
Gives us this type definition
- aSimpleListFunction : unit -> (int * int * int) list
What that means is that the function takes unit (void) and returns a list with 3 int elements in it. If we increased the size of the list returned by the function the signature would change accordingly
Returning A Sequence
let aSimpleSequenceFunction() = seq { 1..3}
Gives us this type definition
- aSimpleSequenceFunction : unit -> seq<int>
What that means is that the function takes unit (void) and returns a sequence of int values
Returning A Function (Higher Order Functions)
In F# it is perfectly legal to return functions too. Any function that takes or returns another function is known as a Higher Order Function. Here is an example.
let doubleFunction x = x * 2 let aSimpleHigherOrderFunction = doubleFunction
Which gives us this type definition
- aSimpleHigherOrderFunction : (int -> int)
Since our “aSimpleHigherOrderFunction” simply returns the original function “doublerFunction” it is that original function “doubleFunction” that is the one that is returned, and as such it is that functions signature that we see in the FSI window. So we get a function that takes an int and returns an int. As stated earlier functions are shown as “(“ and “)”, though watch out for tuple which also use braces, but they also use “*” so they should be easy to spot. They will take the form “(a *b)”
While we are on the subject of Higher Order Functions, we should probably mention the more common use cases examples, which would likely involve one of the many functions available within the List/Sequence modules. For example List.Map, which has the type signature :
- List.map : (‘T -> ‘U) -> ‘T list -> ‘U list
Which takes the following input parameters
A function that takes a generic parameter ‘T, and returns a new generic value ‘U
- Takes a list of generic values ‘T
- Which returns a new list of generic values ‘U
So lets see an example of this in action.
Here is a small example that will negate a list of numbers, where we declare a “negate” function that takes a value and returns a new value. So this will work with List.Map, as its type signature fits with what List.Map requires.
let negate x = -x let newList = List.map negate [1;2;3;4]
We could of course make this a bit more succinct by using a lambda function, which would give us this:
let newList = List.map (fun x -> -x) [1;2;3;4]
Understanding Functions That Taken Parameters
Ok so we have now seen what return values look like, so lets start adding in some input parameters into the mix.
Generic Function
So let’s start with a generic function, where we let the F# type inference system decide what the type will be.
Here is the function we will be using:
let aSimpleGenericFunction x = ()
Which when inspected in the FSI Window gives us this type definition
- aSimpleGenericFunction : x:’a –> unit
Which as you can see has a strange “ ’a “ type for the parameter named X. What is this, well in F# that is how generics are represented. So this function is completely generic as far as the input parameter goes, and simply returned unit “()”
So since it is completely generic these are all valid calls to the function:
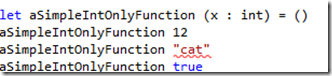
aSimpleGenericFunction 12 aSimpleGenericFunction "cat" aSimpleGenericFunction true
Taking A Single Parameter
So what about when we don’t want to use generics and want to specify the type we want, how do we do that. Well we can do that as follows:
let aSimpleIntOnlyFunction (x : int) = ()
Which when inspected in the FSI Window gives us this type definition
- aSimpleIntOnlyFunction : x:int -> unit
Which as you can is a function that takes a single int value, and simply returned unit “()”
So since we have now locked down the type accepted as an input parameter to this function, we can’t pass in anything other than a single int value.
Taking Several Parameters
So how about we now look at taking a few parameters, for the sake of simplicity I will fix the types allowed. So here is an example:
let aMultipleParamsFunction (x : int) (y: string) = ()
Which when inspected in the FSI Window gives us this type definition
- aMultipleParamsFunction : x:int -> y:string -> unit
Which as you can is a function that takes a int and a string value, and simply returned unit “()”
Taking A Mix Bag Of Parameters
Ok so we now have the basics covered, lets mix it up a bit by looking at what you we get if we create a pretty full on function that takes a variety of the types we have looked as so far:
let theUberFunction (a : int option) (b : int list) (c : string) (d) = ()
Which when inspected in the FSI Window gives us this type definition
- theUberFunction : a:int option -> b:int list -> c:string -> d:’a -> unit
Which as you can is a function that takes
- A int option
- A int list
- A string
- A generic type
And returns unit “()”
Just for completeness here is what an example of calling this function looks like
theUberFunction (Some 12) [1;2;3] "dog" { Name = "Alf" }
Taking Parameters And Having A Non Unit Return Value
So lets finish this section with a truly weird function, which looks like this:
let someCrazedFunction (a:int) (b:string) (c:SimplePerson)
(d: Collections.List<int>) (e) = (a,b,c,d,e)
Ok, I have gone a bit over the top with this one, but the point is it is still totally valid, and you may see things like this in the wild, although I do not think this is a great idea at all, we would likely tuple the parameters instead. Let’s continue though and see what the signature for this one looks like. The first 4 parameters should be pretty obvious, and the last one is a generic one, but what would the return value of this be? Lets find out.
- someCrazedFunction :
a:int ->b:string ->
c:SimplePerson ->
d:List<int> -> e:’a -> int * string * SimplePerson * List<int> * ‘a
This looks a little nuts, but lets just break it down. From left to right (which is the correct way to read F# signatures)
This function is one that takes the following input parameters:
- An Int
- A String
- A SimplePerson record
- A list of Ints
- A generic value
And it returns a tuple of int * string * SimplePerson * List<int> * ‘a
I deliberately made this one a bit strange, so that we could see a somewhat weird signature
One To Watch Out For
You may on occasion see a function that includes a “inline” keyword.This F# keyword is used to integrate the function directly into the calling code. Here are some examples of where you might see inline used:
type WrapInt32() =
member inline this.IncrementByOne(x) = x + 1
static member inline Increment(x) = x + 1
...
...
let inline Increment x = x + 1
The thing is, using the inline keyword, DOES effect the signature of a function, so that is why I am bringing this up in this blog post.
For example lets say I had this function
let PrintAsFloatingPoint number =
printfn"%f" (float number)
I think this would pretty easy to guess the signature of, it takes an ‘a generic, and the last line of the function is a printfn one, which returns Unit, that was my guess The actual signature is
- PrintAsFloatingPoint : number:int –> unit
This is due to the F# tylpe inference system deducing a input type, in this case int.
But let’s see what happens when we use the inline keyword. So sticking with the same example:
let inline InlinePrintAsFloatingPoint number =
printfn"%f" (float number)
Which when examined in the FSI Window has the following signature, which is very very different:
- inline InlinePrintAsFloatingPoint : number: ^a -> unit when ^a : (static member op_Explicit : ^a -> float)
Using the inline keyword forces the F# type inference system to infer that the function can take a statically resolved typed parameter. This means that the function accepts any type that has a conversion to float. That is why we see the use of the “op_Explicit” and “^a –> float” (the ^a specifies types that must be resolved at compile time not at runtime) which makes sure it is convertible to float.
Interestingly enough if we actually lock down the type for the number parameter for both these demo functions to an int, so we have these new functions:
let PrintAsFloatingPoint (number :int) =
printfn"%f" (float number)
let inline InlinePrintAsFloatingPoint (number :int) =
printfn"%f" (float number)
And now look at the type signatures, we can see that they are identical.
- PrintAsFloatingPoint : number:int –> unit
- inline InlinePrintAsFloatingPoint : number:int -> unit
So beware inline may catch you out
It would probably be worth explaining the apparent ambiguity in function signatures.
For instance,
int -> int -> intis a function that takes two ints and returns an int, but it could also be read as a function that takes an int, and returns a function that takes an int and returns an int. And it’s actually the same thing, because of currying and partial application…Thomas, good call I’l try and slot that in when I get a minute. Think I have taken on slightly too much right now, arggghhh
let aSimpleListFunction() = [1,2,3]
it means that function returns list with one element (tuple). If you need 3 elements list it should be:
let aSimpleListFunction() = [1; 2; 3]
about
let aSimpleHigherOrderFunction = doubleFunction
if we don’t use () and function doesn’t have parameters, it’s actually not function, but value
if we want function, we should write:
let aSimpleHigherOrderFunction() = doubleFunction
and signature will be:
val aSimpleHigherOrderFunction : unit -> (int -> int)
F# Functions vs. Values discussion: http://stackoverflow.com/questions/3554750/f-functions-vs-values