F#12 : Arrays

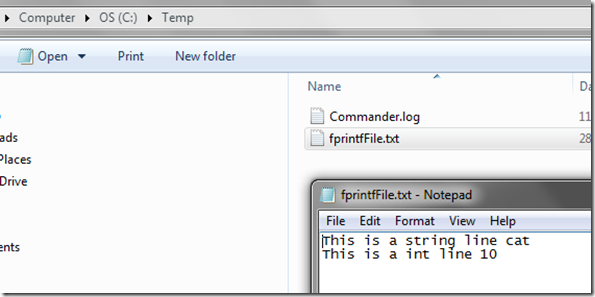
No language would be complete without arrays (at least in my opinion). They are an excellent structure. F# is of course no fool, and includes them (as you would expect), so this blog will concentrate on looking at using arrays in F#

 

Creating Arrays

There are several ways to create arrays, just as there were with List and Sequences. You have the following choices

• Inline initialisation (where you provide the values)
• Using comprehensions (that we say with List and Sequences)
• Using the Array module itself which has several array creation functions

Here are some examples

/// The empty array
let emptyArray = [| |]

// inline array values
let fruitArray = [| "bananna"; "apple"; "pear"; "mango"; "rambutan"; "lychee" |]

// use list comprehension syntax
let numberArray = [| 1 .. 10 |]

/// An array containing only the words "hello" and "world"
let onlyLArray = [| for word in fruitArray do
                    if word.StartsWith("l") then 
                        yield word |]

// An array initialized by index and containing the the number squared
// using the Array module directly
let generatorArray = Array.init 11 (fun n -> n * 2) 

 

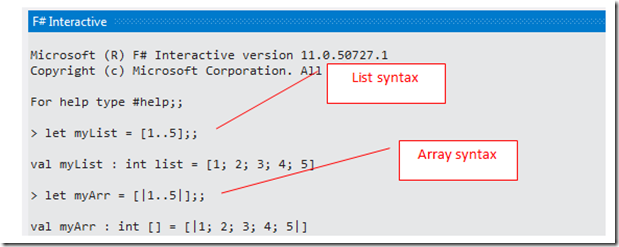
Which when run looks like this:

 

BEWARE

Now you need to be slightly careful with your syntax (a lot of F# is like this), there is really not much difference between how you declare lists and arrays. See the screen shot below. The key difference is the use of the “[|” and “|]”which arrays use and lists do not. One to watch for. We will also see some more quite similar syntax to this further down the line, but that is when we look at passive/active patterns, but we aint there yet, so lets not cloud the waters with even more syntax for now.

 

Arrays Of Arrays

We can also make arrays of arrays, which can be done as follows:

/// The empty array of arrays
let emptyArrayOfArrays = [|  [| |] ; [| |]  |]
 
// array of arrays
let arrayOfArrays = [|   [| 1;2;3|] ; [| 4;5;6|] |]

Which when run looks like this:

 

 

Multi Dimensional Arrays

As you would expect we can also create different dimensioned arrays. There is however no inline syntax (array literal as it is known in F#) for working with 2d arrays (or higher, yes F# supports them up to 4D, if you are mad enough to need it F# supports it).

We can however use one of the built in F# operators. Here are some examples that show you how to create 2D and 3D arrays:

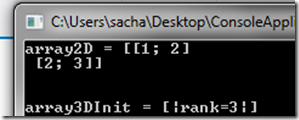
// use the array2D operator
let array2D = array2D [ [ 1;2]; [2;3]]

// 3d array
let array3DInit = Array3D.init 3 3 3 (fun a b c -> a * 2) 

 

Which when run looks like this:

Everything looks cool with the 2d array, but what is the weird “[|rank=3|]” gibberish. That is actually just do with the printfn function and a bit of a red herring if we try and execute the 3d array line in the FSI window, we see the truth.

 

Which is as expected a 3d array, which is expressed as “int [,,]”, a 2d int array would have just been “int [,]”. The rank simply tells us the dimension count

 

As can be seen here with a 4D array (heaven forbid you need one):

 

NOTE:

It should be noted that the following modules have way less available functions than the rather more common Array F# module

• Array2D
• Array3D
• Array4D

 

Indexing Into Arrays

So now that we have seen how to create arrays, we should see how we can get values out of array elements. It is just worth noting that arrays in F# ARE 0 index based.

Here are some examples, showing how to index into single dimension arrays, and arrays of arrays, and a 2D array.

 

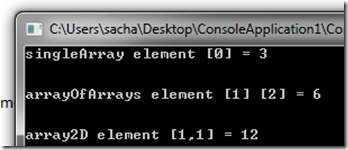
// single array
let singleArray = [|  1;2;3;4;5;6 |]


// array of arrays
let arrayOfArrays = [|   [| 1;2;3|] ; [| 4;5;6|] |]


// use the array2D operator
let array2D = array2D [ [ 1;2;3;4;5]; [11;12;13;14;15]]


printfn "singleArray element [0] = %A" singleArray.[2]
printfn "\r\n"
printfn "arrayOfArrays element [1] [2] = %A" arrayOfArrays.[1].[2]
printfn "\r\n"
printfn "array2D element [1,1] = %A" array2D.[1,1]

Which when run looks like this:

 

See how we need to index into arrays using the “.[0]” (where 0 is the index” syntax. This also applies for arrays of arrays. However for multidimensional arrays, we use the “[1,1]” syntax.

 

Mutating Array Element State

So now that you have seen how to index into arrays, you are probably wondering how you can change the state of an array element. In F# this is done with the assignment operator “<-“.

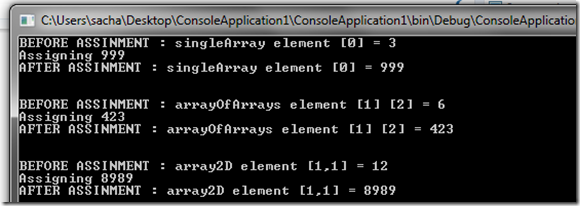
Here are some examples, showing how to assign new values into single dimension arrays, and arrays of arrays, and a 2D array.

// single array
let singleArray = [|  1;2;3;4;5;6 |]


// array of arrays
let arrayOfArrays = [|   [| 1;2;3|] ; [| 4;5;6|] |]


// use the array2D operator
let array2D = array2D [ [ 1;2;3;4;5]; [11;12;13;14;15]]


printfn "BEFORE ASSINMENT : singleArray element [0] = %A" singleArray.[2]
printfn "Assigning 999"
// ************ Assign new value *********************
singleArray.[2] <- 999
printfn "AFTER ASSINMENT : singleArray element [0] = %A" singleArray.[2]
printfn "\r\n"

printfn "BEFORE ASSINMENT : arrayOfArrays element [1] [2] = %A" arrayOfArrays.[1].[2]
printfn "Assigning 423"
// ************ Assign new value *********************
arrayOfArrays.[1].[2] <- 423
printfn "AFTER ASSINMENT : arrayOfArrays element [1] [2] = %A" arrayOfArrays.[1].[2]
printfn "\r\n"
        
printfn "BEFORE ASSINMENT : array2D element [1,1] = %A" array2D.[1,1]
printfn "Assigning 8989"
// ************ Assign new value *********************
array2D.[1,1] <- 8989
printfn "AFTER ASSINMENT : array2D element [1,1] = %A" array2D.[1,1]

 

Which when run will give the following results

 

 

Slicing Arrays

Sometimes you may also want to slice arrays to only grab a certain section of the original array. F# has built in support for this, it is called an array slice.

You may choose to slice an original array like this:

• specify both lower and upper bound, which will copy only those elements between your lower/upper bounds
• specify lower bound, which will copy only those elements above your lower bound
• specify upper bound, which will copy only those elements below your upper bond
• specify wild card, which will in effect copy the entire array

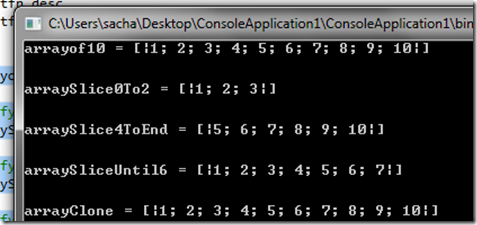
Here is how it is done, in practice

let arrayof10 = [|1..10|]

// Specify lower and upper bound for slice
let arraySlice0To2 = arrayof10.[0..2]

// Specify lower bound only for slice
let arraySlice4ToEnd = arrayof10.[4..]

// Specify upper bound only for slice
let arraySliceUntil6 = arrayof10.[..6]

// Specify wild card, which clones array
let arrayClone = arrayof10.[*]

        

printfn "arrayof10 = %A" arrayof10
printfn "\r\n"
printfn "arraySlice0To2 = %A" arraySlice0To2
printfn "\r\n"
printfn "arraySlice4ToEnd = %A" arraySlice4ToEnd
printfn "\r\n"
printfn "arraySliceUntil6 = %A" arraySliceUntil6
printfn "\r\n"
printfn "arrayClone = %A" arrayClone

Which when run gives the following results

The Array Module

As with List and Sequence, Arrays are a very important type in F#, as such it should be no surprise that they too have good MSDN documentation. As such just as I have stated with List and Sequences, it would be fruitless me just regurgitating what is already available on MSDN. There is no point to that.

The F# Array module MSDN documentation can be found right here : http://msdn.microsoft.com/en-us/library/ee370273.aspx

I think it is always nice to see a few examples, though, so in fitting with what I have been so far in this series, I will show a few demos, but you should refer to MSDN for the full list of the Array module functions.

I have picked a few random functions which I think are cool, and useful, that said the F# Array module hold many fascinating and useful functions.

 

Find

Returns the first element for which the given function returns true. Raise KeyNotFoundException if no such element exists.

FindIndex

Returns the index of the first element in an array that satisfies the supplied condition. Raises KeyNotFoundException if none of the elements satisfy the condition.

 

Here is a small demo that covers both Find, and FindIndex, where we try and Find the element value when the element contains 2, and also its index.

let arrayof10 = [|1..10|]
let element = Array.find (fun elem -> elem = 3) arrayof10
let index = Array.findIndex (fun elem -> elem = 3) arrayof10
printfn "The first element that is 3 is %d and its index is %d." element index

Which when run looks like this:

 

 

ForAll

Tests whether all elements of an array satisfy the supplied condition.

Here is a small sample that wants all the array elements to be > 0

//simple way of writing it 
let allAbove0 = (Array.forall (fun elem -> elem > 0) [| 0; 1; 2; 3 |])
printfn "(Array.forall (fun elem -> elem > 0) [| 0; 1; 2; 3 |]) = %A" allAbove0

let allAbove0 = (Array.forall (fun elem -> elem > 0) [| 1; 2; 3 |])
printfn "(Array.forall (fun elem -> elem > 0) [| 1; 2; 3 |]) %A" allAbove0

Which when run produces the following results:

 

We could also rewrite this use partial application (which is a F# topic I have not covered just yet), but essentially it allows us to partially apply the parameters to a function, then bind that function, and then at some later point in time supply the remaining parameters. Which in the example below, would be the final parameter (the array itself)

//use partial application
let allPositive = Array.forall (fun elem -> elem > 0)
let allAbove0 = (allPositive [| 0; 1; 2; 3 |])
printfn "(allPositive [| 0; 1; 2; 3 |]) = %A" allAbove0

let allPositive = Array.forall (fun elem -> elem > 0)
let allAbove0 = (allPositive [| 1; 2; 3 |])
printfn "(allPositive [| 1; 2; 3 |]) = %A" allAbove0

 

Init

Creates an array given the dimension and a generator function to compute the elements.

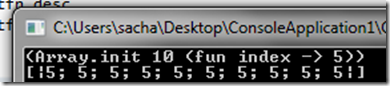
As you can imagine this is especially useful when you want to initial an array with your own choice of seed data. Here is an example where we fill the entire array with the integer value 5 (god knows why you would want a whole array of 5’s but meh).

printfn "(Array.init 10 (fun index -> 5))" 
let array = (Array.init 10 (fun index -> 5))
printfn "%A" array

Which when run produces the following results:

 

Partition

Splits the collection into two collections, containing the elements for which the given predicate returns true and false respectively.

Here is a small example where we want the results partitioned based on whether the array elements are > 3 or not. So we would expect to get a tuple returned with 2 arrays in it, where one array held elements who’s values are < 3, and second tuple value should be an array where the array element values are >= 3

 

let arrayOf10 = [|0..10|]
let tupleResults = Array.partition (fun element -> element < 3) arrayOf10
    
printfn "let arrayOf10 = [|0..10|]"
printfn "let tupleResults = Array.partition (fun element -> element < 3) arrayOf10"
printfn "tupleResults fst = %A" (tupleResults |> fst)
printfn "tupleResults snd = %A" (tupleResults |> snd)

 

Which when run produces the following results

F#11 : Sequences

Last time we looked at the List module, and we now proceed to look at the sequence module. You will in fact see a lot of similarities with the sequence module compared to the list module. The main difference between F# lists and F# sequence is pretty much the same as it is in C#|VB .NET, A list is every element and is all loaded (greedily) into memory, whist sequences are lazy and will only be evaluated as needed. This is much the same as it is with IEnumerable<T> in standard .NET. In fact sequences are represented by the seq<‘T> type, which is an alias for IEnumerable<T>. Therefore, any .NET Framework type that implements System.IEnumerable can be used as a sequence.

Creating Sequences

In F# there are several ways in which you can create Lists, shown below are a few examples.

• Create a simple list containing 1 to 10
• Create a simple list creating odd numbers between 1 and 10, which is achieved using a step operator
• Using a for loop to create a list

 

You will definitely see similarities between the code below and the code we saw in the last post when creating lists. In fact what makes a list is the existence of the “[“ and “]” braces, whilst sequence uses “{“ and “}” style braces.

 

let prettyPrint desc seq =
    printfn desc
    printfn "%A" seq
         
 
//simple sequence
let seq1 = {1 .. 10 }
//simple list, with step value
let seq2 = {1 ..2..10 }
//simple list, with step value, and this time use the "seq" keyword
let seq3 = seq {1 ..2..10 }
//using for loops to create sequences
let seq4  = seq { for i in 1 .. 10 do yield i * i }
//using for loops to create sequences, but use lambda
let seq5  = seq { for i in 1 .. 10 -> i * i }
//how about creating 2d sequences
let Create2dArray (height, width) = 
    seq { for row in 0 .. width - 1 do 
            for col in 0 .. height - 1 do 
            yield (row, col)
    }
let seq6 = Create2dArray (5,5)

let seq7 = seq { for i in 1 .. 20 do if i = 10 then yield i }

prettyPrint "let seq1 = {1 .. 10 }" seq1
prettyPrint "let seq2 = {1 ..2..10 }" seq2
prettyPrint "let seq3 = seq {1 ..2..10 }" seq3
prettyPrint "let seq4  = seq { for i in 1 .. 10 do yield i * i }" seq4
prettyPrint "let seq5  = seq { for i in 1 .. 10 -> i * i }" seq5
prettyPrint "let Create2dArray (height, width) = 
                seq { for row in 0 .. width - 1 do 
                        for col in 0 .. height - 1 do
                        yield (row, col)
                }
                let seq6 = Create2dArray (5,5)\r\n" seq6

prettyPrint "let seq7 = seq { for i in 1 .. 20 do if i = 10 then yield i }\r\n" seq7

Which when run will give the following results

Yield!

As well as the Yield keyword we have already seen, we can also use the yield! keyword, to yield a single outer sequence. This is similar to IEnumerable.SelectMany. Lets see an example of this is action, which may help you to understand the differences between Yield and Yield! (pronounced yield bang).

Lets see an example of the difference between Yield and Yield!

let prettyPrint desc seq =
    printfn desc
    printfn "%A" seq
         

//yield sequence
let yieldBangSeq = seq { for i in 0..10..100 do
                            yield! seq {i..1..i*5}}

 
//yield sequence
let yieldSeq = seq { for i in 0..10..100 do
                        yield seq {i..1..i*5}}
    
prettyPrint "let yieldBangSeq = seq { for i in 0..10..100 do
                        yield! seq {i..1..i*5}}\r\n" yieldBangSeq
printfn "\r\n\r\n"

prettyPrint "let yieldSeq = seq { for i in 0..10..100 do
                        yield seq {i..1..i*5}}\r\n" yieldSeq

Which when run looks like this:

It can be seen that the example above that uses the Yield!  actually only produces one final sequence, whilst the the one that uses Yield produces sequences within sequences.

If we examine the types of the 2 bound values it may help to solidify this a bit further.

 

 

See how the Yield! version is a single Seq<int>, whilst the regular Yield one is a Seq<Seq<int>>.  Lets now turn our attention to what it would look like if we used the results of both of these values. Here is some revised code:

//yield sequence
let yieldBangSeq = seq { for i in 0..10..100 do
                            yield! seq {i..1..i*5}} |> Seq.take 3 |> Seq.toList

 
//yield sequence
let yieldSeq = seq { for i in 0..10..100 do
                        yield seq {i..1..i*5}} |> Seq.take 3

Which when run will give us the following results:

 

Consuming A Sequence

It is fairly easy to consume a sequence once you have one, it can be done as simply as follows:

// Recursive isprime function. 
let isprime n =
    let rec check i =
        i > n/2 || (n % i <> 0 && check (i + 1))
    check 2

let aSequence = seq { for n in 1..100 do if isprime n then yield n }
for x in aSequence do
    printfn "%d" x

Where we can use a simple for loop (this will be covered in a later blog post), to iterate (lazily) over the sequence. Here is the results of running this:

 

 

The Sequence Module

As we saw last time with the List module, the Sequence module is also a VERY important module in F#, and just as with the List module, the Sequence module gets some good loving from the Microsoft team. So just as before I will not be able to bring much to the table that they do not already cover. I will cover a few example which as before I borrowed (um stole) from the MSDN web site for the Sequence module which is found at : http://msdn.microsoft.com/en-us/library/dd233209.aspx

There are way too many functions for me to include in this blog. As with the List module MSDN is actually very good for Sequences, which sadly can not be said of all aspects of F# development. For Sequences you are fine though, MSDN is rad and Gnarly.

Some examples

I have included a couple of examples here just so you can get a feel for the Sequence module

 

Seq.Take / Seq.toList

Here is an example where we take the first 10 elements from a sequence, and then toList the sequence, which creates a non lazy in memory List.

let prettyPrint desc seq = 
    printfn desc
    printfn "%A" seq


let bigSeq = seq { 1..1000}
let smallerList = bigSeq |> Seq.take 10 |> Seq.toList

prettyPrint "let bigSeq = seq { 1..1000}\r\nlet smallerList = bigSeq |> Seq.take 10 |> Seq.toList" smallerList

Which when run gives the following results:

 

 

Seq.iter / Seq.pairwise / Seq.map

Here is an example where we do the following:

• The Seq.pairwise function generates a sequence of tuples of consecutive squares, { (1, 4), (4, 9), (9, 16) … }
• The seq.map allow us to run a lambda across each element in the sequence
• The Seq.iter allows us to iterate over the sequence an element at a time

 

let printSeq seq1 = Seq.iter (printf "%A ") seq1; 
printfn "" 
let seqPairwise = Seq.pairwise (seq { for i in 1 .. 10 -> i*i })
printSeq seqPairwise

printfn "" 
let seqDelta = Seq.map (fun elem -> snd elem - fst elem) seqPairwise
printSeq seqDelta

 

Seq.compareWith

compareWith allow us to to compare sequences (that is all the elements in a sequence). Here is an example:

 

let sequence1 = seq { 1 .. 10 }
let sequence2 = seq { 10 .. -1 .. 1 }

// Compare two sequences element by element. 
let compareSequences = Seq.compareWith (fun elem1 elem2 ->
    if elem1 > elem2 then 1
    elif elem1 < elem2 then -1
    else 0) 

let compareResult1 = compareSequences sequence1 sequence2
match compareResult1 with
| 1 -> printfn "Sequence1 is greater than sequence2."
| -1 -> printfn "Sequence1 is less than sequence2."
| 0 -> printfn "Sequence1 is equal to sequence2."
| _ -> failwith("Invalid comparison result.")

 

Which when run will give the following results:

 

As I say the Sequence module has so many goodies in it, I could not possible cover them all here. Luckily the Sequence module is very well documented using the MSDN link, so use that it is your friend.

F#10 : Lists

Any serious programming you do in any language will always involve lists. As such you will be pleased to know that F# has very very good support for Lists, by way of its List module. A list in F# is an ordered, immutable series of elements of the same type.

 

Creating Lists

In F# there are several ways in which you can create Lists, shown below are a few examples.

• Create an empty list
• Create a simple list containing 1 to 10
• Create a simple list creating odd numbers between 1 and 10, which is achieved using a step operator
• Using a for loop to create a list

let prettyPrint desc list =
    printfn desc
    printfn "%A" list
        

//empty list
let listEmpty = []
//simple list
let list1 = [1 .. 10 ]
//simple list, with step value
let list2 = [1 ..2..10 ]
//using for loops to create lists
let list3 = [for i in 1 .. 10 -> i*2 ]



prettyPrint "let listEmpty = []" listEmpty
prettyPrint "let list1 = [ 1 .. 10 ]" list1
prettyPrint "let list2 = [ 1 .. 2..10 ]" list2
prettyPrint "[ for i in 1 .. 10 -> i*2 ]" list3

Which when run will give the following results:

 

 

List Comprehensions

The last example in the one above showed how to use a for loop to create a list, which is very cool, but there is something even more cool and powerful within the F# toolbox, which are “List Comprehensions”.

“List Comprehensions” are a powerful technique that allow you to create lists by using pretty much and of the standard F#, which includes functions/loops/conditions etc.

Lets continue to have a look at example of how we might construct lists using list comprehensions.

let is2 x = match x with
    | 2 -> "YES"
    | _ -> "NO"



//yield directly
let list1 = [
    yield 1;
    yield 2;
    yield 3;
]

//yield numbers between 1 and 20 where we use the
//Math.Pow function to return a new number
let list2 = [for i in 1.0 .. 20.0 do
                yield Math.Pow(i,2.0)
            ]
    
//yield only numbers between 1 and 20 that 
//can be divided by 5
let list3 = [
                for i in 1 .. 20 do
                    if i % 5 = 0 then
                        yield i
            ]


//yields YES/NO strings depending on
//whether source int = 2 or not
let list4 = [for i in 1 .. 5 ->
                is2 i
            ]

Which prints this when run

Some Useful List Operators

Cons Operator

We can use the cons operator “::” to append values to an existing list, so suppose we had this list

let list1 = [1;2;3;4]
let list2 = 42 :: list1

Which gives this result

 

Concat Operator

Another quite useful operator is the “@” operator, which allows you to concatenate lists that have the same type. So for example if we had this

let list1 = [1;2;3;4]
let list2 = [5;6;7;8]
let list3 = list1 @ list2

We would get the following results

 

 

The List Module

I don’t think I am overplaying things when I say that the List module is a pivotal module in the F# landscape. I fact the MSDN documentation for the List module is extremely good when compared to other areas in F#. As such I don’t think I will be able to add much value to some of the examples found on MSDN, but I will include a few here for your convenience, but for more information you should examine MSDN : http://msdn.microsoft.com/en-us/library/dd233224.aspx

 

Properties

A list has a number of useful properties which are quite useful, which are shown in the table below:

 

Property	Type	Description
Head	‘T	The first element
Empty	‘T list	A static property that returns an empty list of the appropriate type
IsEmpty	bool	true if the list has no elements
Item	‘T	The element at the specified index (zero-based)
Length	int	The number of elements
Tail	‘T list	The list without the first element

 

Where we can see example usage of these as follows:

let list1 = [ 1; 2; 3 ]

// Properties
printfn "list1.IsEmpty is %b" (list1.IsEmpty)
printfn "list1.Length is %d" (list1.Length)
printfn "list1.Head is %d" (list1.Head)
printfn "list1.Tail.Head is %d" (list1.Tail.Head)
printfn "list1.Tail.Tail.Head is %d" (list1.Tail.Tail.Head)
printfn "list1.Item(1) is %d" (list1.Item(1))

 

Which when run, will give the following results:

 

There are also many (too many for one blog, but  we will go through a few, for the rest MSDN is actually very on) functions that are available in the F# List module. In fact the MSDN page for the List module is excellent, and has an example for each list module function, as such I would urge you to peruse MSDN for a look at what you can do.

The MSDN page is here : http://msdn.microsoft.com/en-us/library/ee353738.aspx

We will however look at a few examples here, for fun like (note I have taken most of these examples straight from MSDN)

 

Filter

Returns a new collection containing only the elements of the collection for which the given predicate returns true.Here is a trivial example that only picks even numbers from a list to produce a new list

let evenOnlyList = List.filter (fun x -> x % 2 = 0) [1; 2; 3; 4; 5; 6]

Which when run looks like this:

 

Find

Returns the first element for which the given function returns true. In this example since a list of 1 to 100 contains 5, 5 is the 1st number that is divisible by 5 so it is the return value

let isDivisibleBy number elem = elem % number = 0
let result = List.find (isDivisibleBy 5) [ 1 .. 100 ]

Which when run looks like this:

 

Forall

Tests if all elements of the collection satisfy the given predicate. In this example the entire list needs to contain 0s to get a true return value.

let isAllZeroes list = List.forall (fun elem -> elem = 0.0) list
printfn "%b" (isAllZeroes [0.0; 0.0])
printfn "%b" (isAllZeroes [0.0; 1.0])

Which when run looks like this:

 

 

Iteri

Applies the given function to each element of the collection. The integer passed to the function indicates the index of element.

let data = ["Cats";"Dogs";"Mice";"Elephants"]
data |> List.iteri (fun i x -> printfn "item %d: %s" i x)

Which when run looks like this:

 

 

SortWith

Sorts the given list using the given comparison function.

let list1 = [ ""; "&"; "&&"; "&&&"; ""; "|"; "||"; "|||" ]
printfn "Before sorting: "
list1 |> printfn "%A" 

//custom sorting function
let sortFunction (string1:string) (string2:string) =
    if (string1.Length > string2.Length) then
        1
    else if (string1.Length  printfn "After sorting:\n%A"

Which when run looks like this:

 

 

There are loads of useful functions in the list module this is a mere fraction of what can be found, have a look there are some very useful functions to be found

 

 

Pattern Matching Lists

It is also fairly trivial to pattern match against List values, where we can simply do something like this:

In this example we are matching 2 cases

1. List which has a head and tail, which we match using the syntax head :: tail (you don’t have to use the labels “head” and “tail”, these are arbitrary labels)
2. Empty list

let printIt desc x = 
    printfn "%A %A" desc x

let patternMatchAList list =
    match list with
    | head :: tail -> 
        printIt "head=" head
        printIt "tail=" tail
    | [] -> ()

patternMatchAList [1;2;3;4;5]
printfn "\r\n\r\n"
patternMatchAList [1;2]
printfn "\r\n\r\n"
patternMatchAList [1]
printfn "\r\n\r\n"

Which gives these results

 

Small Look At Recursion With Lists

No discussion on F# Lists and pattern matching would be complete without talking about recursion. Now recursion is something I will be dedicating an entire post to, but for now lets see what it takes to write a recursive function that works over a list in F#.

So we have the following code:

let printIt desc x = 
    printfn "%A %A" desc x

let rec printList list =
    match list with
    | h :: t -> 
        printIt "head=" h
        printIt "tail=" t
        printList t
    | [] -> ()


printList [1;2;3;4;5]

Note the use of the rec keyword, that tells the F# compiler that this function will be recursive. Without that keyword, a recursive function call is a compile time error, albeit not a great error message (at least not in my opinion)

 

So lets see the results of running the good example shown just above with the following list [1;2;3;4;5]

It can be seen that our pattern matching works just fine, and it terminates when it matches an empty list as expected

F#9 : Option types

If C# there is a concept of null for reference types and Nullable<T> class for value types (structs). For value type this can take one of the following 2 forms (for demo purposes I am using a int type here, but the type could be any value type)

• Nullable<int>
• int?

 

These are both equivalent.

The Nullable<T> class exposes a few helper properties and methods that make it easier to work with null and value types. These are as following

Property/Method	Description
HasValue	Gets a value indicating whether the current Nullable<T> object has a valid value of its underlying type.
Value	Gets the value of the current Nullable<T> object if it has been assigned a valid underlying value.
GetValueOrDefault()	Retrieves the value of the current Nullable<T> object, or the object’s default value.
GetValueOrDefault(T)	Retrieves the value of the current Nullable<T> object, or the specified default value.

 

In F# there is something slightly different to this, in the form of an Option type, which is more F# friendly type, that prefers to not deal in terms of null and not null, but rather prefers to deal with things in terms of “Can hold a value of a type” or “May not have a value”. This does sound like Nullable<T> I give you that, but it is a F# type after all, so you can expect it to ok to use in F# things, such as pattern matching etc etc.

Another thing to note with F’’#s Option type is that is may be used for any type, not just value types. This is different from the .NET Nullable<T> which may only be used with value types.

The value None is used when an option does not have an actual value. Otherwise, the expression Some( … ) gives the option a value. The values Some and None can obviously be used in pattern matching, which we will see an example of in this post.

Like Nullable<T>, the F# Option type has several helper properties / methods, which are shown in the table below.

 

Property/Method	Type	Description
None	‘T option	A static property that enables you to create an option value that has the None value.
IsNone	bool	Returns true if the option has the None value.
IsSome	bool	Returns true if the option has a value that is not None.
Some	‘T option	A static member that creates an option that has a value that is not None.
Value	‘T	Returns the underlying value, or throws a NullReferenceException if the value is None.

 

Additional Helpers

There is an Option module that contains a few more helpers for dealing with Option types in F#.  You can read more about this here: http://msdn.microsoft.com/en-us/library/ee370544.aspx

 

Creating Options

So now that we know what Option types are, how do we go about creating them. Lets see some examples shall we. Note in this example I has used the helper methods IsSome / IsNone. Personally I think pattern matching is a better way to go, as it will make you match against all cases including the None case.

In fact I will show you just how easy it is to get something wrong, when dealing with Option types, should you choose to use the helper methods, but first lets see an example of the ok case (though pattern matching is still preferred).

So lets say we had this code:

let someInt = Some(43)
let someString = Some("cat")

let printTheOption (opt :Option<'a>) =
    printfn "Actual Option=%A" opt
    printfn "IsNone=%b, IsSome=%b Value=%A\r\n\r\n" opt.IsNone opt.IsSome opt.Value

printfn "let someInt = Some(43)"
printfn "let someString = Some(\"cat\")"
printfn "printTheOption (someInt)"
printTheOption someInt
printfn "printTheOption (someString)"
printTheOption someString

This would give us the following results (as expected)

 

But what about we try that again using this code, where we have a None for the value of the Option we will pass to the “printTheOption” function:

let demoNone = None

let printTheOption (opt :Option<'a>) =
    printfn "Actual Option=%A" opt
    printfn "IsNone=%b, IsSome=%b Value=%A\r\n\r\n" opt.IsNone opt.IsSome opt.Value

printfn "let demoNone = None"
printfn "printTheOption demoNone"
printTheOption demoNone

This time if we attempt to run this code we get this result:

 

As you can see we have an issue here. The issues is that we tried to get the passed in Option value using the Option.Value helper property, which is this case was None, so we got a NullReferenceException. This is shown in the table above,when you use the helper properties and methods you may get Exceptions thrown such as this one. Ok you could use the IsNone method, but that would then ripple through your code, and you would be forever checking the value using this, when you could just use a nice clean pattern match, job done.

If you can’t relate to this, ask yourself how many times you have had to check for null when using C#, for me that is a fair amount. This has even given rise to people bringing functional constructs like the Maybe Null Monad into regular.NET  code, but this certainly isn’t part of the BCL.

 

Luckily we can avoid these issues by using pattern matching which we look at next.

 

 

Pattern Matching Options

So now that we have seen the dangers of using the helper methods/properties, and how easy it is to forget about the None case. So lets now turn our attention to how we could avoid these Exceptions by simply  using some simple pattern matching such as that shown here:

let printTheOption (opt :Option<'a>) =
    match opt with
    | Some a -> printfn "opt is Some, and has value %A" a
    | None -> printfn "opt is None"

let demoNone = None
let someInt = Some 1
let someString = Some "crazy dude in the monkey house"

printTheOption demoNone
printTheOption someInt
printTheOption someString

My personal feeling is that the pattern matching is actually way more readable, than code that would be littered with IsSome / IsNone all over the place. That is of course a personal feeling, but the fact that we have covered all our bases here in this one simple pattern matched function, can not be ignored.

Here is the result of running this:

 

Option vs Null

So we have talked about F#s Option compared to Nullabe<T> and we know that an Option type can be used with any type whilst Nullable<T> can only be used with value types (structs). But what about Option types versus regular reference types in .NET. Well one huge win for F# Option is that when you use a reference type in .NET you are really dealing with a pointer reference, which as such can be set to null. The object type however is still the same as it was declared as, which may hold a valid reference to an object on the heap, or may be null.

So it is total ok to write something like this

string s1 = "cats";
int s1Length = s1.Length;

string s2 = null;
int s2Length = s2.Length;

This will compile just fine, for the reasons I stated above. However when we run this we will get a NullReferenceException, for which we would apply defensive programming to protect all code from the possible presence of null. This does become tedious pretty quickly even if you have a nice little guard class that will test a value and handle it / throw some more meaningful Exception.

This small screen shot uses LinqPad so it may look a bit strange if you have not seen LinqPad before, but trust me you would still get the same result in a different IDE.

 

 

Now lets what the equivalent code would look like in F#, which would be this

let s1 = "Cats"
let s1Length = s1.Length;

let s2 = None
let s2Length = s2.Length;

//excplicily string typed None
let s3 = Option.None
let s3Length = s3.Length;

Here is what this looks like in Visual Studio. It can be seen that this is an immediate compile time error, where sis considered a completely different type, and as such has no concept of a “Length” property.

 

Equality With Options

Option types are considered equal they hold the same type, and that the type they hold are equal, which is subject to the equality rules of the held type.

So this sort of thing would cause an immediate compile time error in F#

let o1 = Some 1
let o2 = Some "Cats"

printfn "o1=o2 : %b" (o1 = o2)

This will give this result

 

Whilst this would work as expected since the types are the same

let o1 = Some "Cats"
let o2 = Some "Cats"
let o3 = Some "cats"

printfn "o1=o2 : %b" (o1 = o2)
printfn "o2=o3 : %b" (o2 = o3)

Which yields this result

F#8 Discriminated Unions

 

OK so our F# journey continues. We have looked at some of the basic building block types such as Records/Tuples, it is now time to look at Discriminated Unions.

Discriminated unions provide support for values that can be one of a number of possible values. The possible values are known as “union cases”, and take the form shown below

case-identifier1 [of [ fieldname1 : ] type1 [ * [ fieldname2 : ] type2 …]

Don’t worry if this syntax looks scary, what it really boils down to is having a label such that each case can be recognized (discriminated) from the others, and a type for the union case. The label name has certain rules around it such as

• Must start with an uppercase letter
• Can be an identifier including the union case type name itself. Which cane be a little confusing, but does have the benefit of describing the union case quite well

 

Here is an example of a bad identifier

 

And here is what something may look like when using a label identifier which is the same as the union case, which as previously stated is perfectly valid

type LabelUnionType = Int of int | String of string

Constructing Discriminated Unions

So how does one construct a union case. Well there are various ways, you are able use one of the following approaches

 

let currentLabelUnionType1 =   13
printfn "let currentLabelUnionType1 =   13" 
printfn "%O" currentLabelUnionType1

   
let currentLabelUnionType2 =  Int 23
printfn "let currentLabelUnionType2 =  Int 23" 
printfn "%O" currentLabelUnionType2
printfn "%A" currentLabelUnionType2

 
let currentLabelUnionType3 =  "Cat"
printfn "let currentLabelUnionType3 =  \"Cat\"" 
printfn "%O" currentLabelUnionType3
printfn "%A" currentLabelUnionType3
 
let currentLabelUnionType4 =  String "Cat"
printfn "let currentLabelUnionType4 =  String \"Cat\"" 
printfn "%O" currentLabelUnionType4
printfn "%A" currentLabelUnionType4

Which when run may produce the following results when run through the printfn function (I am either using a %A or %O printfn formatter below)

 

You can pretty much use any type in the union cases, such as

• Tuples
• Records
• Other types

The only rule is that the type must be defined before your union case can use it

Here is an example that uses a tuple type in the union cases

 

type unionUsingTuples = CCY of (int * String) | Rates of (int * decimal)
.....
.....
let tupledUnion = (12, "GBP")

 

Empty Unions

You may also use empty unions. Which are ones where you do not specify a type. This makes them much more like standard .NET enum values. Here is an example of that.

type Player = Cross | Nought
....
....
let emptyUnion = Cross

What About Similar Cases Across Types

The eagle eyed amongst you may see a problem. What would happen if we had something like this

type PurchaseOrders = Orders of (string * int) | Empty
type ClientOrders = Orders of (string * int) | Empty

This causes us a problem doesn’t it. How would we distinguish between these discriminated union types? Well luckily we can just use a fully qualified approach to this, so we can simply do this, and everything will work as expected. It should be noted that you could take this one step further and include the module name if a module is involved (we will see more on this later, in a subsequent article)

let purchaseOrders = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1)
let clientOrders = ClientOrders.Orders ("scrubbing brush", 23)

Discriminated Unions Equality

As with a lot of F# types, Discriminated Unions are only considered equal if

• The length of their union cases match
• The types of their union cases match
• The values of their union cases match

 

 

Are not equal

Here is an example where things are not considered equal

let purchaseOrders1 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1)
let purchaseOrders2 = PurchaseOrders.Orders ("10 pack of disks", 1)

printfn "purchaseOrders1 = purchaseOrders2 %A" (purchaseOrders1 = purchaseOrders2)

Which looks like this when run

 

Are Equal

Here is an example where things are considered equal. This is kind of inline with regular .NET code, you know if the members are the same, they have the same values and there is the correct number of them they are pretty much the same thing (if we ignore hash codes that is)

let purchaseOrders1 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1)
let purchaseOrders2 = PurchaseOrders.Orders ("box of 100 scrubbing brushes", 1)

printfn "purchaseOrders1 = purchaseOrders2 %A" (purchaseOrders1 = purchaseOrders2)

Which looks like this when run

 

It should be noted that we can not use equality when we have to fully qualified union types as they are different types, so this would not work

 

 

Pattern Matching Discriminated Unions

As with most of F# you are able to pattern match against discriminated union. Shown below is a small function that accepts a Card discriminated union and will print the union cases it was called with and simply returns a Unit type (void if you recall that from previous articles in this series)

type Card = ValueCard of int | Jack | Queen | King | Ace
....
....
let cardFunction card = 
    match card with
    | ValueCard i -> printfn "its a value card of %A" i
    | Jack -> printfn "its a Jack"
    | Queen -> printfn "its a Jack"
    | King -> printfn "its a Jack"
    | Ace -> printfn "its a Ace"
    () //return unit

   
//shows you how to pass it in without a Let binding
do cardFunction (Card.ValueCard 8)

//or you could use explicit Let binding if you do desire
let aceCard =  Ace
do cardFunction aceCard

Here is the result of running the pattern matching code above

So Just Exactly What Is Going On Behind The Scenes There

So we have now seen some examples of how Discriminated Unions work. So what do you think would happen if we had a F# library that used Discriminated Unions and we chose to use that from C#/VB.NET. Do you think that would work. The answer is sure it would. I will be doing a whole post on Interop somewhere down the line, but I just thought it may be fun to visit part of that right now for Discriminated Unions as they are so different from anything we see in standard .NET programming.

So lets take the card example above, which was this code:

type Card = ValueCard of int | Jack | Queen | King | Ace

And the run it through a decompiler, such as Reflector / DotPeek (whatever you have essentially). I used DotPeek and got this C# code for that single line of F#. So as you can see the F# compiler is doing a lot of work to esnure the F# types will interop nicely with regular .NET such as C#/VB .NET.

using Microsoft.FSharp.Core;
using System;
using System.Collections;
using System.Diagnostics;
using System.Runtime.CompilerServices;
using System.Runtime.InteropServices;

[CompilationMapping(SourceConstructFlags.Module)]
public static class Program
{
  [EntryPoint]
  public static int main(string[] argv)
  {
    return 0;
  }

  [DebuggerDisplay("{__DebugDisplay(),nq}")]
  [CompilationMapping(SourceConstructFlags.SumType)]
  [Serializable]
  [StructLayout(LayoutKind.Auto, CharSet = CharSet.Auto)]
  public class Card : IEquatable<Program.Card>, IStructuralEquatable, 
	IComparable<Program.Card>, IComparable, IStructuralComparable
  {
    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public int Tag
    {
      [DebuggerNonUserCode] get
      {
        return this._tag;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public bool IsValueCard
    {
      [DebuggerNonUserCode] get
      {
        return this.get_Tag() == 0;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public static Program.Card Jack
    {
      [CompilationMapping(SourceConstructFlags.UnionCase, 1)] get
      {
        // ISSUE: reference to a compiler-generated field
        return Program.Card._unique_Jack;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public bool IsJack
    {
      [DebuggerNonUserCode] get
      {
        return this.get_Tag() == 1;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public static Program.Card Queen
    {
      [CompilationMapping(SourceConstructFlags.UnionCase, 2)] get
      {
        // ISSUE: reference to a compiler-generated field
        return Program.Card._unique_Queen;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public bool IsQueen
    {
      [DebuggerNonUserCode] get
      {
        return this.get_Tag() == 2;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public static Program.Card King
    {
      [CompilationMapping(SourceConstructFlags.UnionCase, 3)] get
      {
        // ISSUE: reference to a compiler-generated field
        return Program.Card._unique_King;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public bool IsKing
    {
      [DebuggerNonUserCode] get
      {
        return this.get_Tag() == 3;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public static Program.Card Ace
    {
      [CompilationMapping(SourceConstructFlags.UnionCase, 4)] get
      {
        // ISSUE: reference to a compiler-generated field
        return Program.Card._unique_Ace;
      }
    }

    [CompilerGenerated]
    [DebuggerNonUserCode]
    [DebuggerBrowsable(DebuggerBrowsableState.Never)]
    public bool IsAce
    {
      [DebuggerNonUserCode] get
      {
        return this.get_Tag() == 4;
      }
    }

    static Card()
    {
    }

    [CompilationMapping(SourceConstructFlags.UnionCase, 0)]
    public static Program.Card NewValueCard(int item)
    {
      return (Program.Card) new Program.Card.ValueCard(item);
    }

    [CompilationMapping(SourceConstructFlags.UnionCase, 1)]
    public static Program.Card get_Jack()
    {
      // ISSUE: reference to a compiler-generated field
      return Program.Card._unique_Jack;
    }

    [CompilationMapping(SourceConstructFlags.UnionCase, 2)]
    public static Program.Card get_Queen()
    {
      // ISSUE: reference to a compiler-generated field
      return Program.Card._unique_Queen;
    }

    [CompilationMapping(SourceConstructFlags.UnionCase, 3)]
    public static Program.Card get_King()
    {
      // ISSUE: reference to a compiler-generated field
      return Program.Card._unique_King;
    }

    [CompilationMapping(SourceConstructFlags.UnionCase, 4)]
    public static Program.Card get_Ace()
    {
      // ISSUE: reference to a compiler-generated field
      return Program.Card._unique_Ace;
    }

    public static class Tags
    {
      public const int ValueCard = 0;
      public const int Jack = 1;
      public const int Queen = 2;
      public const int King = 3;
      public const int Ace = 4;
    }

    [DebuggerTypeProxy(typeof (Program.Card.ValueCard\u0040DebugTypeProxy))]
    [DebuggerDisplay("{__DebugDisplay(),nq}")]
    [Serializable]
    [SpecialName]
    public class ValueCard : Program.Card
    {
      [CompilationMapping(SourceConstructFlags.Field, 0, 0)]
      [CompilerGenerated]
      [DebuggerNonUserCode]
      public int Item
      {
        [DebuggerNonUserCode] get
        {
          return this.item;
        }
      }
    }

    [SpecialName]
    internal class ValueCard\u0040DebugTypeProxy
    {
      [CompilationMapping(SourceConstructFlags.Field, 0, 0)]
      [CompilerGenerated]
      [DebuggerNonUserCode]
      public int Item
      {
        [DebuggerNonUserCode] get
        {
          return this._obj.item;
        }
      }
    }
  }
}

Recursive Cases (Tree Structures)

Discriminated Unions may also be used in a recursive manner, where the union itself may be used as one of the types in one or more of the cases. This makes Discriminated Unions very suitable for modelling tree like structures, such as:

• Mathematical Expressions
• Abstract syntax trees
• Xml

 

MSDN actually has some good examples on this, so I decided to do some more borrowing (stealing) here (thanks MSDN). The following paragraphs are taken from the the following MSDN Url:

http://msdn.microsoft.com/en-us/library/dd233226.aspx

 

In the following code, a recursive discriminated union is used to create a binary tree data structure. The union consists of two cases, Node, which is a node with an integer value and left and right subtrees, and Tip, which terminates the tree.

The Tree structure for myTree in the example below is as shown in the figure here :

 

 

And here is how we would model the myTree using Discriminated Unions. Notice how we include the Discriminated Union itself as one of the union cases. In this case the union cases are either

1. A tip (empty union case, acts like standard enum in .NET)
2. Or a 3 valued tuple of int, Tree, Tree

The other thing to note is that the sumTree function is marked with a “rec” keyword. What does this magic incantation do to our function? Well it marks the sumTree functions as one that will be called recursively. Without the “rec” keyword on the sumTree function, the F# compiler would complain. In this case the compiler would issue the following error.

 

 

But we are good citizens, and will use the correct key words to support our use case, so onwards we go 

type Tree =
    | Tip
    | Node of int * Tree * Tree
....
....
....
....
let rec sumTree tree =
    match tree with
    | Tip -> 0
    | Node(value, left, right) ->
        value + sumTree(left) + sumTree(right)
let myTree = Node(0, 
                    Node(1, 
                        Node(2, Tip, Tip), 
                        Node(3, Tip, Tip)), 
                    Node(4, Tip, Tip))
let resultSumTree = sumTree myTree

printfn "Value of sumTree is %A" resultSumTree

 

Which when run will show the following results

 

MSDN also has one other good example that I thought might be worth stealing (yes I am being blatant about it now. I think as long as you guys/girls get something out of this borrowed example which I clearly say is borrowed, I am all like ‘meh’). Lets see that example here:

type Expression = 
    | Number of int
    | Add of Expression * Expression
    | Multiply of Expression * Expression
    | Variable of string
....
....
....
let rec Evaluate (env:Map<string,int>) exp = 
    match exp with
    | Number n -> n
    | Add (x, y) -> Evaluate env x + Evaluate env y
    | Multiply (x, y) -> Evaluate env x * Evaluate env y
    | Variable id    -> env.[id]

let environment = Map.ofList [ "a", 1 ;
                                "b", 2 ;
                                "c", 3 ]

// Create an expression tree that represents 
// the expression: a + 2 * b. 
let expressionTree1 = Add(Variable "a", Multiply(Number 2, Variable "b"))

// Evaluate the expression a + 2 * b, given the 
// table of values for the variables. 
let result = Evaluate environment expressionTree1

printfn "Value of sumTree is %A" result

Which when run will show the following results

F#7 : Records

So we continue our journey into more of the F# types. This time we will be looking at Record types.

 

How Do I Create A Record

When you create a new F# record, it may remind you of anonymous objects in C#. Here is how you create them. I think they are quite similar to anonymous objects in C#, so if you have used C#, F#s records should not be that hard to get into.

It starts by creating a new type for the record. The type definition lists the name of the properties and also the type of the properties, this can be seen below.

Once you have a record type definition you re free to bind a new instance to a value use Let. Again an example of this can be seen below, where we bind a new record using a Let binding, and we also print the property values of the record instance to the console output.

type Person = { Age : int; Sex: string; Name:string; }  
....
....
....
....
let sam = { Age = 12; Sex="Male"; Name ="Sam" }
printfn "let sam = { Age = 12; Sex=\"Male\"; Name=\"Sam\" }" 
printfn "Person with Age is %i and Sex is %s and Name is %s" sam.Age sam.Sex sam.Name

which gives this result

 

How Do I Alter/Clone A Record

You are able to clone and alter a record, which is typical done as follows:

//clone and alter sam to become new Person tom
let sam = { Age = 12; Sex="Male"; Name ="Sam" }
let tom = { sam with Name="Tom" }
printfn "let tom = { sam with Name=\"Tom\" }" 
printfn "Person with Age is %i and Sex is %s and Name is %s" tom.Age tom.Sex tom.Name

Which gives this result

Note how we used the “with” keyword when creating the new tom person instance. This form of the record expression is called the “copy and update record expression”. Another choice you could use (again we will be covering this in more detail in a later post) is use a mutable property in your record type. Records are immutable by default; however, you can also explicitly specify a mutable field.

Here is an example, notice how I have created a new type which has a mutable property called MutableName. By defining a mutable field, I am allowed to update the value of the MutableName property of the record, which you can do using the “<-“ operator. Which simply allows a new value to be assigned.

type MutableNamePerson = { Age : int; Sex: string; mutable MutableName:string; }   
....
....
....
....
//create
let sam = { Age = 12; Sex="Male"; MutableName ="Sam" }
printfn "let sam = { Age = 12; Sex=\"Male\"; Name=\"Sam\" }" 
printfn "Person with Age is %i and Sex is %s and Name is %s" sam.Age sam.Sex sam.MutableName
//update
sam.MutableName <- "Name changed"
printfn "sam.MutableName <- \"Name changed\"" 
printfn "Person with Age is %i and Sex is %s and Name is %s" sam.Age sam.Sex sam.MutableName
    

Which has this result

 

 

Record Equality

Record types are only equal if ALL the properties are considered the same. Here is an example

type Person = { Age : int; Sex: string; Name:string; }   
....
....
....
....
let someFunction p1 p2 =
    printfn "p1=%A, and p2=%A, are they equal %b" p1 p2 (p1=p2)


let sam =  { Age = 12; Sex = "Male"; Name = "Sam" }
let john = { Age = 12; Sex = "Male"; Name = "John" }
let april = { Age = 35; Sex = "Female"; Name = "April" }
let sam2 = { Age = 12; Sex = "Male"; Name = "Sam" }
do someFunction sam john
do someFunction sam april
do someFunction sam sam2

And here is the result

Pattern Matching Records

It is of course possible to use pattern matching (a discussion for another day),  which is a core F# technique, to match against Record types. Here is an example

type Person = { Age : int; Sex: string; Name:string; }  
.....
.....
.....
.....
let someFunction (somePerson :Person) =
    match somePerson with
    | { Name="Sam" }    -> printfn "Sam is in the house"
    | _                 -> printfn "you aint Sam, get outta here clown"


let sam = { Age = 12; Sex="Male"; Name ="Sam" }
let john = { Age = 12; Sex="Male"; Name ="John" }
do someFunction sam
do someFunction john

Which has the result

Methods And Properties

It is also possible to add extra members to records. Here is an example where we add a “Details” property to allow the full details of the record to be obtained by using a single property (much as the we could achieve by overriding the ToString() method, but more on OO techniques later on ok)

Note that if you tried to add a member to the record type definition as shown in this screen shot you will get a strange error

This is easily solved by simply putting the record property definitions on a new line, and making sure the member starts on a new line too, and watch that indenting (whitespace), as it is all important in F#

type Person = 
    { Age : int; Sex: string; Name:string; }   
    member this.Details = this.Age.ToString() + " " + this.Sex.ToString() + " " + this.Name
....
....
....
....
let sam =  { Age = 12; Sex = "Male"; Name = "Sam" }
printfn "sam Details=%s" sam.Details

 

Which has the result

F#6 : Tuples

So our journey into F# continues. The next coupe of posts will be about F# types that may or may not have standard .NET equivalents. This post will be talking about tuples.

 

What Are Tuples

A tuple is a grouping of unnamed but ordered values, possibly of different types.

 

Creating Tuples

Tuples are very easy to create, we simply do something like the following. Notice how I have created a mixed bag of tuples here, some are Ints, and others are strings, and we can also mix and match both the types and the number of values

//Creating Tuples
let a = (1,2)
let b = (1,"cat")
let c = (1,"cat")
let d = (1,"cat", 'c')

 

Generic Tuples

Functions accepting tuples can accept generic tuples without any issues as well. The F# type inference system will happily deal with deducing the correct types for the tuple. Here is an example

let someFunction tup = 
    let (x,y) = tup
    printfn "x is %A and y is %A" x y

do someFunction ("cat","dog")
do someFunction (11,12)

And here is the results of running the above, where it can be seen that the someFunction function had no problem accepting and dealing with different typed tuples

Tuple Signatures

Up until now we have not touched on understanding F# signatures at all yet, it is in fact a topic i have decided to dedicate a whole blog post too, as I feel it is sufficiently complicated enough to warrant its own blog post. We are however where we are, which is the here and now, and we are exploring tuples, so for  now I just wanted to demonstrate what a tuple signature would look like.

So lets say I had declare the following tuples in a FSI window

//Creating Tuples
let a = (1,2)
let b = (1,"codfather")
let c = (1,"c", 12.5)

And then I evaluated them in the FSI window, we would see something like this:

val a : int * int = (1, 2)
val b : int * string = (1, "codfather")
val c : int * string * float = (1, "c", 12.5)

This is interesting, we can see a couple of things here, namely:

• The round braces are not part of the type signature
• The F# type system is able to correctly infer the type based on the values contained in the tuple itself
• The comma is replaced with a “*”

So just so are crystal clear, a tuple which looks like this

let a = (1,2)

Will have type signature of

int * int

 

Exploding Tuples

So we have seen how we can create tuples, but what about exploding or deconstructing them back into individual values. Is that possible? Yeah sure it is. As before lets start by looking at some examples:

 

//Exploding Tuples
let (a,b) = (1,2)

printfn "(a,b) = (1,2), so value of 'a' should be 1, and it is =%i,\r\n 'b' should be 2, and it is =%i" a b

//using wildcard, essentially dont create an unnessecary value binding if you are
//not interested in it
let (_,z) = (1,2)
printfn "grabbing last value from (1,2) which is = %i" z


//how about some strongly Let bindings
let (a,b :string) = (1,"cat")
printfn "grabbing (1,\"cat\") which has values = %i %s" a b

let (a :int,b :string) = (1,"cat")
printfn "grabbing (1,\"cat\") which has values = %i %s" a b


let (a ,b, c) = (1,"cat", 'c')
printfn "grabbing (1,\"cat\",'c') which has values = %i %s %c" a b c


//using built in helpers
let first = fst (1, 2)
printfn "grabbing fst from (1,2) which has values = %i" first

let second = snd (1, 2)
printfn "grabbing 2nd from (1,2) which has values = %i" second

Where the results are printing to a standard Console window, as follows:

 

 

Using Let

So that was the output, but how did we get the individual parts? Well everything you need is in the code above, but lets go through one example. Suppose we had a tuple like this:

(1,2)

And I wanted to get the values of both the tuple values bound to some new individual values, we could just do this:

let (a,b) = (1,2)

We can also choose to only grab the values we truly care about, which is done using a wildcard for the unwanted parts. Which makes sure that no unnecessary value binding occurs. Here is an example:

let (_,z) = (1,2)

Using inbuilt tuple functions

There is also inbuilt support for obtaining the first and second values from a tuple. Which can be done using the “fst” and “snd” functions. There is no support for anything other than the 2st 2 (these are probably the most common cases). “fst” and “2nd” can be used as follows:

let first = fst (1, 2)
let second = snd (1, 2)

Now I want to draw your attention to a special case, which is when we may have a mismatch with the number of value that we are attempting to explode into individual values. So that would be something like the example here:

//oh oh wrong number of values in let binding compiler tells us
let (a ,b) = (1,"cat", 'c')

You can see that the tuple itself actually contains 3 values, but the Let binding only has 2 values, so the compiler warns us about this, as you can see in the screen shot below

 

 

 

Creating New Tuples

You may want to create new tuples from existing tuples, this is easy enough, here is an example

let oldOne = (1,2)
let (x,y) = oldOne
let newOne = (x+1,y+1)
printfn "original = %A, and we did this (x+1,y+1)\r\n to obtain newOne = %A" oldOne newOne

Which gives this output

 

 

Tuple Equality

Tuples are ONLY considered to be equal if

• They have the same number of values
• ALL the values are considered equal (Obviously this could include custom Equals methods, or custom IEquatable implementations etc etc)

Lets see some dead simple example shall we.

printfn "(1,2) = (3,4) = %b" ((1,2) = (3,4))
printfn "(1,2) = (1,2) = %b" ((1,2) = (1,2))
printfn "('a','b') = ('a','b') = %b" (('a','b') = ('a','b'))
printfn "('a','b') = ('a','c') = %b" (('a','b') = ('a','c'))

which results in this

 

In fact if your tuples have different lengths and you are attempting to compare them using the equals operator “=” you will get a warning

 

Pattern Matting Tuples

We have not gone into pattern matching yet, but we will see an entire post on this subject later on. For now just know that it is a way to match again input parameters. You can do this against tuples, which is done as follows:

let someFunction tup = 
    match tup with
    | 1,2 -> printfn "you passed (1,2)"
    | _,_ -> printfn "you passed some other tuple"
    
do someFunction (11,12)
do someFunction (4,5)
do someFunction (1,2)
do someFunction (13,23)

Which gives the following results

F#5 : Operators

Now I had intended to write a 1/2 decent blog post on F# operators, but then I had a think about this, and too be honest I could not actually see too much merit in simply reiterating what was already freely available on MSDN where it lists ALL of the F# operators.

 

You can find a full list of all the F# operators and symbols on this MSDN page:

http://msdn.microsoft.com/en-us/library/dd233228.aspx

 

If you follow this link the 1st thing you will realise is that F# has a lot of operators and symbols, far too many for me to include in a single blog post. With that in mind I have taken my intention of creating a 1/2 decent blog post of operators, and decided to cut back the scope a bit to only include a discussion of the most common operators, so I guess you could say this blog will only be a 1/4 or 1/8 of a decent post, for which I humbly apologise.

 

Now before we start I just wanted to say that I am only going to go through the most common operators, you will more than likely have to examine the MSDN link I included at the top of this post, when you really start to use F#, but for now I hope the ones I have chosen to concentrate on will be ok to get us started.

Oh one last thing, I am going to be pretty honest about this, so here goes, the brief description for each of the operators has been lifted directly from MSDN, its one of those cases, when you are just meh “could not have said it better myself”, so  didn’t and just borrowed um stole the stuff from MSDN.

 

Arithmetic Operators

The following table summarizes the binary arithmetic operators

 

+ Addition

Unchecked. Possible overflow condition when numbers are added together and the sum exceeds the maximum absolute value supported by the type.

– Subtraction

Unchecked. Possible underflow condition when unsigned types are subtracted, or when floating-point values are too small to be represented by the type.

* Multiplication

Unchecked. Possible overflow condition when numbers are multiplied and the product exceeds the maximum absolute value supported by the type.

/ Division

Division by zero causes a DivideByZeroException for integral types. For floating-point types, division by zero gives you the special floating-point values +Infinity or -Infinity. There is also a possible underflow condition when a floating-point number is too small to be represented by the type.

% Modulus

Returns the remainder of a division operation. The sign of the result is the same as the sign of the first operand.

** Exponentiation

Possible overflow condition when the result exceeds the maximum absolute value for the type. The exponentiation operator works only with floating-point types.

Demo

Here is a small demo of the Arithmetic operators listed above

//Arithmetic operators
printfn "25 + 25 = %i" (25 + 25)
printfn "75 - 25 = %i" (75 - 25)
printfn "12 * 12 = %i" (12 * 12)
printfn "100 / 4 = %i" (100 / 4)
printfn "101 %% 10 = %i" (101 % 10)
printfn "2 ** 3 = %f" (2.0 ** 3.0)

And here is the result of running this:

Binary Operators

The following table shows the binary comparison operators that are available for integral and floating-point types. These operators return values of type bool.

= Equals

This is not an assignment operator. It is used only for comparison. This is a generic operator.

> greater than

This is a generic operator.

< less than

This is a generic operator.

>= greater than or equal to

This is a generic operator.

<= greater than or equal to

This is a generic operator.

<> Not Equals

This is a generic operator.

 

Here is a small demo of the Binary operators listed above

//Binary operators
printfn "25 = 25 = %b" (25 = 25)
printfn "26 > 25 = %b" (26 > 25)
printfn "26 < 25 = %b" (26 < 25)
printfn "26 >= 25 = %b" (26 >= 25)
printfn "26 <= 25 = %b" (26 <= 25)
printfn "'a' <= 'b' = %b" ('a' <> 'b')
//how about a more complex example, a tuple
printfn "(1,'a') = (2,'a') = %b" ((1,'a') = (2,'a'))
printfn "(1,'a') = (1,'a') = %b" ((1,'a') = (1,'a'))
printfn "Some(1) = Some(2) = %b" (Some(1) = Some(2))
printfn "Some(2) = Some(2) = %b" (Some(2) = Some(2))

And here is the result of running this:

 

 

Boolean Operators

The following table summarizes the Boolean operators that are available in the F# language. The only type supported by these operators is the bool type.

not

Boolean negation

|| or

Boolean OR

&& and

Boolean AND

Here is a small demo of the Boolean operators listed above

//Boolean operators
printfn "not true = %b" (not true)
printfn "true || false = %b" (true || false)
printfn "true && true = %b" (true && true)
printfn "true && false = %b" (true && false)

And here is the result of running this:

Bitwise Operators

The following table describes the bitwise operators that are supported for unboxed integral types in the F# language.

&&& and

Bitwise AND operator. Bits in the result have the value 1 if and only if the corresponding bits in both source operands are 1.

||| or

Bitwise OR operator. Bits in the result have the value 1 if either of the corresponding bits in the source operands are 1.

^^^ XOR

Bitwise exclusive OR operator. Bits in the result have the value 1 if and only if bits in the source operands have unequal values.

~~~ negation

Bitwise negation operator. This is a unary operator and produces a result in which all 0 bits in the source operand are converted to 1 bits and all 1 bits are converted to 0 bits.

<<< bit shift left

Bitwise left-shift operator. The result is the first operand with bits shifted left by the number of bits in the second operand. Bits shifted off the most significant position are not rotated into the least significant position. The least significant bits are padded with zeros. The type of the second argument is int32.

>>> bit shift right

Bitwise right-shift operator. The result is the first operand with bits shifted right by the number of bits in the second operand. Bits shifted off the least significant position are not rotated into the most significant position. For unsigned types, the most significant bits are padded with zeros. For signed types, the most significant bits are padded with ones. The type of the second argument is int32.

Here is a small demo of the Bit shift operators listed above

//Bit shift operators

//&&& and
printfn "2 &&& 4 (which is 0010 &&& 0100, should be 0) = %X" (2 &&& 4)
printfn "2 &&& 3 (which is 0010 &&& 0011, should be 2) = %X" (2 &&& 3)
 
//||| or
printfn "2 ||| 4 (which is 0010 ||| 0100, should be 6) = %X" (2 ||| 4)
printfn "2 ||| 3 (which is 0010 ||| 0011, should be 3) = %X" (2 ||| 3)
   

//^^^ xor
printfn "2 ^^^ 4 (which is 0010 ^^^ 0100, should be 6) = %X" (2 ^^^ 4)
printfn "2 ^^^ 3 (which is 0010 ^^^ 0011, should be 1) = %X" (2 ^^^ 3)

//^^^ negate
printfn "~~~4 (which is not 0100, should be 1011 (B hex), or 11 decimal) = %X" (~~~4)

//<<< bit shift left
printfn "4 <<< 1 (which is 0100 <<< by 1 place left , should be 1000 (8 hex), or 8 decimal) = %X" (4 <<<  1)

//>>> bit shift right
printfn "4 >>> 1 (which is 0100 >>> by 1 place right , should be 0010 (2 hex), or 2 decimal) = %X" (4 >>>  1)

And here is the result of running this:

 

 

Operator Overloading

As I have already mentioned there will be times when you do need to implement your own operator logic. In other .NET languages this would be achieved by supplying your own operator overloads. In should come as no surprise that you need to do the same thing in F#. I did not want to get onto classes and OO just yet, but it kind of fits the current discussion so lets see how you might implement your own operators in a custom F# type.

Again I have stolen this from MSDN. The following code illustrates a vector class that has just two operators, one for unary minus and one for multiplication by a scalar. In the example, two overloads for scalar multiplication are needed because the operator must work regardless of the order in which the vector and scalar appear.

type Vector(x: float, y : float) =
   member this.x = x
   member this.y = y
   static member (~-) (v : Vector) =
     Vector(-1.0 * v.x, -1.0 * v.y)
   static member (*) (v : Vector, a) =
     Vector(a * v.x, a * v.y)
   static member (*) (a, v: Vector) =
     Vector(a * v.x, a * v.y)
   override this.ToString() =
     this.x.ToString() + " " + this.y.ToString()

  For more information you can see MSDN : http://msdn.microsoft.com/en-us/library/dd233204.aspx

F#4 : Let / Use / Do Bindings

In this post we will look at F# bindings, in particular we will look at Let / Use / Do. Now you may be asking yourself what a binding is, and since we have not really covered it yet, now would be a good time to talk about this.

Quite simply a binding associates an identifier with a value or function.

 

Let

You use the let keyword to bind a name to a value or function. There are actually subtlety different uses of Let, where one is declared as a top level in a module, and then another is where we define some sort of local context. Here is an example of both of these:

module DemoModule =

    let someFunction =
        let a = 1
        let b = 2
        a * b

 

We would be able to access the someFunction using a fully qualified name such as DemoModule.someFunction, but the nested Let bindings (a,b) are only accessible to the top level Let binding. You would typically see more cases where we are using the Let binding to declare some inner module values, so lets concentrate our efforts there (though it is still important to know you can use Let at module level).

So let’s have a look at a few more examples

 

let aString ="this is a string"
let aInt = 12
let aDecimal = 12.444
let aPiFunction () = Math.PI
let aSquareRootFunction (x) = Math.Sqrt(x)
let aFullyTypedSquareRootFunction (x :float) = Math.Sqrt(x)
let a,b = "a","tuple"

It can be seen that we are able to use the Let binding, to bind to numerous values, that can be of various types such as:

• Integer
• Decimal
• A Function with no input parameters
• A Function with input parameters (where the F# type inference system will correctly choose the Type)
• A Function which has fully qualified parameter types
• A tuple (a tuple of String * String in this case)

 

Another place you may see a Let binding is in a class, but we will cover this in more detail in a later article in this series

 

You can read more about the Let binding using MSDN : http://msdn.microsoft.com/en-us/library/dd233238.aspx

 

Use

The Use binding is quite similar to the Let binding in that it binding a value to the result of an expression. The key difference is that the Use binding is designed to work with IDisposable types and will automatically Dispose of the value when it is no longer in scope. This is quite similar to the .NET using keyword, though I do not believe that the F# Use binding will be exactly the same as the .NET using keyword semantics, as the .NET using keyword is really a try / finally with a Dispose() call in the finally.

We have already seen an example of the Use binding in the last post we did on Formatting Text, but just to remind ourselves lets have a look at that again

use sw = new StreamWriter(@"c:\temp\fprintfFile.txt")
fprintf sw "This is a string line %s\r\n" "cat"
fprintf sw "This is a int line %i" 10
sw.Close()

In this example the Use binding ensures that the StreamWriter will have its Dispose() method called after the sw.Close() call seen above.

 

A couple of points

Use Only Works with IDisposables, and you will get a compilation error should you try and use it with anything else, as shown below

 

As the Dispose() method is called at the end of a Use binding, care should be taken to not return a value that was bound using a Let.

i.e : Don’t do this:

 

let Write =
    use sw = new StreamWriter(@"c:\temp\fprintfFile.txt")
    sw

 

If you absolutely need to pass an IDisposable around that are part of a Use binding, you can use a callback instead. So something like this would work, but I would stop and ask yourself have you got your design right if you are doing this sort of thing

let Write callback =
    use sw = new StreamWriter(@"c:\temp\fprintfFile.txt")
    fprintf sw "Write is writing to the StreamWriter"
    callback sw
    sw

let callback sw = fprintf sw "sw is the StreamWriter"
let disp = Write callback

 

 

Do

Use a do binding is used to execute code without defining a function or value. A Do binding MUST always return Unit (no value / void essentially). In a lot of cases you will be able to omit the Do binding value and things will work just as expected.

Here are some examples of using the Do binding

do printf "doing the do"
//oh oh not a unit
do printf "print a sum %i" 1 + 1
do 1 + 1

 

If I instead show you a screen shot of the code above you will see that the compiler complains if you try and use Do with a Non Unit result.

You have 2 choices as he error message states, which is to either

1. Use the forward pipe operator to pipe the results to ignore
2. Create a Let binding

 

I have shown an example of each of these below:

let x = 1 + 1
do printf "print a sum %i" x
do (1+1 |> ignore)

 

You can read more about the Let binding using MSDN : http://msdn.microsoft.com/en-us/library/dd393786.aspx

 

Let! Use! ad Do!

Although I don’t want to discuss these just yet, you may on occasion see Let! / Use! / Do!, and when you do these are part of what is known as a computation expression. The place you are most likely to see these is within F#s Asynchronous Workflows which we will be going through in one of the final articles. If I man enough I may even attempt to explain how you can create your own “Computation Expression” though they are quite an abstract concept and are quite an advanced topic so now is not the time for them.

F#3 : Formatting text

One of the things you will most likely need to do when you work with any language is format text, and surprise surprise F# is no different.

Since F# is a .NET language we can always make use of Console.WriteLine(..) and String.Format(..) where we could use any of the regular formatters that you have used in your regular .NET code.

However F# also supports a more C syntax like technique which is available within the Core.Printf module. One function within that can be used instead of the Console.WriteLine(..) .NET class usage.

 

The F# equivalent function that you would use to write to the standard output is printfn, which is actually the preferred method when dealing with text formatting in F#.

 

Why is printfn preferred over Console.WriteLine(..) ?

There are several reasons that printfn is preferred, some of the main reasons are shown below:

• Static type checking. Which means if we pass an int value where a string is expected, we are warned about this
• As printfn is a native F# function, is acts just like any other F# function. Where you do certain F# things, such as possibly partially applying the function (which is something we will try and cover a bit more in a subsequent post)
• It will have baked in support for standard F# types

 

Lets just spend a bit more time on the statically typed point above. Consider the following code snippets

// incorrect type
printfn "should be a decimal value %d" "cat"
//this works
printfn "should be a decimal value %d" 42
// incorrect type but works
Console.WriteLine("should be a decimal value {0}" , "cat")


// wrong number of parameters provided
printfn "this only expected 1 arg of type decimal %d" 42 "dog"
// wrong number of parameters provided but works
Console.WriteLine("this only expected 1 arg of type decimal {0}" , 42, "dog")
// this works as expected
printfn "this only expected 2 args of type decimal %d and string %s" 42 "dog"

 

If we now look at a screen shot of this code actually in the Visual Studio IDE, we can indeed see that the lines that we expected to fail are clearly shown as being in error:

 

 

How we use printfn?

So now that we know why we should use printfn, how do we use it?

Well probably the best place to start is by looking at some of the standard formatters available when dealing with values. The following table illustrates the standard operators that are available to you:

I have taken these directly from MSDN : http://msdn.microsoft.com/en-us/library/ee370560.aspx

 

 

Type	Description
%b	Formats a bool, formatted as true or false.
%c	Formats a character.
%s	Formats a string, formatted as its contents, without interpreting any escape characters.
%d, %i	Formats any basic integer type formatted as a decimal integer, signed if the basic integer type is signed.
%u	Formats any basic integer type formatted as an unsigned decimal integer.
%x	Formats any basic integer type formatted as an unsigned hexadecimal integer, using lowercase letters a through f.
%X	Formats any basic integer type formatted as an unsigned hexadecimal integer, using uppercase letters A through F.
%o	Formats any basic integer type formatted as an unsigned octal integer.
%e, %E, %f, %F, %g, %G	Formats any basic floating point type (float, float32) formatted using a C-style floating point format specifications.
%e, %E	Formats a signed value having the form [-]d.dddde[sign]ddd where d is a single decimal digit, dddd is one or more decimal digits, ddd is exactly three decimal digits, and sign is + or -.
%f	Formats a signed value having the form [-]dddd.dddd, where dddd is one or more decimal digits. The number of digits before the decimal point depends on the magnitude of the number, and the number of digits after the decimal point depends on the requested precision.
%g, %G	Formats a signed value printed in f or e format, whichever is more compact for the given value and precision.
%M	Formats a Decimal value.
%O	Formats any value, printed by boxing the object and using its ToString method.
%A, %+A	Formats any value, printed with the default layout settings. Use %+A to print the structure of discriminated unions with internal and private representations.
%a	A general format specifier, requires two arguments. The first argument is a function which accepts two arguments: first, a context parameter of the appropriate type for the given formatting function (for example, a TextWriter), and second, a value to print and which either outputs or returns appropriate text. The second argument is the particular value to print.
%t	A general format specifier, requires one argument: a function which accepts a context parameter of the appropriate type for the given formatting function (a TextWriter)and which either outputs or returns appropriate text. Basic integer types are byte, sbyte, int16, uint16, int32, uint32, int64, uint64, nativeint, and unativeint. Basic floating point types are float and float32.

 

I would recommend you have a  look at that MSDN link, as it contains additional information that may be useful when you need to do some fine grained formatting.

 

So what about creating nice formatting other than standard out

So we have now seen how to write nicely formatted output to the standard output (printfn did this), but what about if we wanted to use formatted string in other places? What if we wanted to bind a string value to a nicely formatted string that we constructed using some of the formatters above, or even wanted to write to a StringBuilder or TextWriter, does F# enable us to do that easily?

Well yes actually it does, you will find a great many other useful functions in the Core.Printf module. The full list at time of writing this post was as follows:

 

Value	Description
bprintf	Prints to a StringBuilder.
eprintf	Prints formatted output to stderr.
eprintfn	Prints formatted output to stderr, adding a newline.
failwithf	Prints to a string buffer and raises an exception with the given result. Helper printers must return strings.
fprintf	Prints to a text writer.
fprintfn	Prints to a text writer, adding a newline.
kbprintf	Like bprintf, but calls the specified function to generate the result. See kprintf.
kfprintf	Like fprintf, but calls the specified function to generate the result. See kprintf.
kprintf	Like printf, but calls the specified function to generate the result. For example, these let the printing force a flush after all output has been entered onto the channel, but not before.
kspintf	Like sprintf, but calls the specified function to generate the result. See kprintf.
printf	Prints formatted output to stdout.
printfn	Prints formatted output to stdout, adding a newline.
sprintf	Prints to a string by using an internal string buffer and returns the result as a string. Helper printers must return strings.

 

I am not going to through all of these but I will go through the most common ones:

 

bprintf

Prints to a StringBuilder.

let builder = new StringBuilder(524288)
Printf.bprintf builder "This will be a string line : %s\r\n" "cat" 
Printf.bprintf builder "This will be a bool line : %b\r\n" true
Printf.bprintf builder "This will be a int line : %u\r\n" 42
Printf.bprintf builder "This will be a hex line : %X\r\n" 255

printfn "%s" (builder.ToString())

This will give this output in a F# Console Application

fprintf

Prints to a text writer.

use sw = new StreamWriter(@"c:\temp\fprintfFile.txt")

fprintf sw "This is a string line %s\r\n" "cat"
fprintf sw "This is a int line %i" 10

sw.Close()

This will result in a file being created in temp

sprintf

Prints to a string by using an internal string buffer and returns the result as a string. Helper printers must return strings.

let result = Printf.sprintf "This will return a formatted string : %s\r\n" "cat" 
printfn "%s" result

This will give this output in a F# Console Application