We continue our journey into F#, and this time we will look at recursion. We have already seen this in a number of places, namely when we talked about Lists and also Pattern Matching. So some of this should be vaguely familiar to you.
Simple Example
Lets start with the most basic example which is typical of what we have seen before. This example simply adds all the elements in a input list.
let rec sumFunction theList =
match theList with
| [] -> 0
| head::tail -> head + sumFunction tail
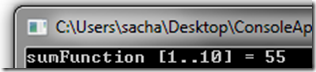
printfn "sumFunction [1..10] = %A" (sumFunction [1..10])
Which when run produces the following output:
There are several take away points from this small code snippet, such as:
- We had to use the “rec” keyword to make the function a recursive one. Without the use of the “rec” keyword the compiler would issue an error
- We put a pattern match in against an empty list.
- We use the “::” (cons) pattern match, such that we are able to match a head and a tail part of a list
So lets now turn our attention to another example, this time we will use the well known Factorial example. Here is a standard way to implement this recursively:
let rec factorial n =
if n = 0 then 1 else n * factorial (n-1)
This looks fine, lets take it for a spin. Lets try run it with input:
printfn "factorial System.Int32.MaxValue = %A" (factorial 10)
Which when run does indeed work just fine, and gives us the following results:
But what about we try a larger problem domain. Let’s try this input instead (see how I am now using Int32.MaxValue)
printfn "factorial System.Int32.MaxValue = %A" (factorial System.Int32.MaxValue)
So what happens now? Let’s see…
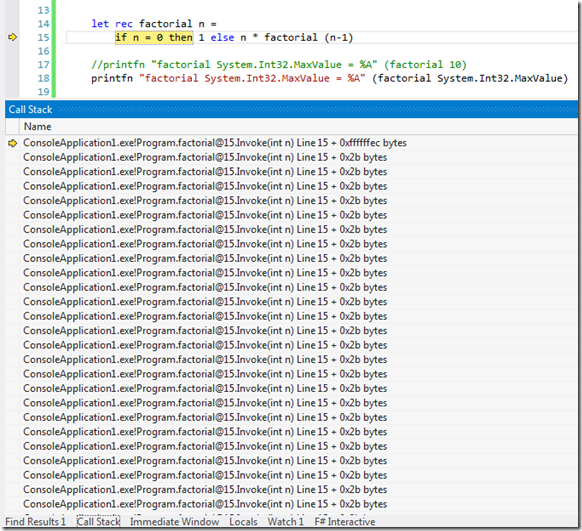
We now get this output, which is um not so great, in fact this is as my old boss would have said a “Cluster Fuck” (pardon my french)
So why did this happen? What did we do wrong?
Well if we turn our attention to the actual Visual Studio IDE and look at the “CallStack” window, we can see some pointers as to why this may be happening.
So we got a whole bunch of calls placed on the stack. The reason for this is actually due to how the code is structured. Let’s examine the code again:
let rec factorial n =
if n = 0 then 1 else n * factorial (n-1)
It can be seen that we use n, but we are also waiting for the result of the recursive call to “factorial” to give us a result, such that we can multiply them together. All of these calls need to be placed somewhere, and they end up being placed on the stack, and eventually we run out of space and get a StackOverFlowException thrown (quite rightly so)
What you should be asking yourself is, is there a better way I could have written my code to avoid this?
Well yes there is, it is called “Tail Recursion”, which also uses a technique called the “Accumulator Pattern”.
Tail Recursion
What does the “Accumulator Pattern” actually mean. For all intents and purposes it really means that we pass an extra value into the function, which is a accumulation value that you can use with each iterative call. This simply change means we no longer need to push things on to the stack to keep the temporary value, obviously the stack is still involved with the recursion itself, but we do not have to push unnecessary values to the stack, As a result the compiler is able to optimize the code.
Ok, lets see the new / better code (for the sake of me not having to wait too long to see a result, I have gone for a small value of “5”, but rest assured you would not get a StackOverFlowException thrown if you use this technique, for larger numbers.
let factorialProducingForLoop x =
// Keep track of both x and an accumulator value (acc)
let rec tailRecursiveFactorial x acc =
if x <= 1 then
acc
else
tailRecursiveFactorial (x - 1) (acc * x)
tailRecursiveFactorial x 1
printfn "factorialProducingForLoop 5 = %A" (factorialProducingForLoop 5)
It can be seen that I have used a non recursive function that is called, that function called contains a nested function which does the recursion, and is called with an initial accumulator value and the original function input value.
Here is the proof that this works fine:
To fully understand the different between the non tail recursive version and the better tail recursive version, let’s have a look at the decompiled source of them (I am using DotPeek to decompile the code, but use what you will):
Non Tail Recursive Version
Here is the decompiled C# code for the non optimized non tail recursive version, where is can clearly be seen that this will heavily involve the stack, which is evident in the Invoke() method shown below, where it can be seen that the Invoke() method is called time and time again
[Serializable]
internal class factorial\u004015 : FSharpFunc<int, int>
{
internal factorial\u004015()
{
}
public override int Invoke(int n)
{
if (n == 0)
return 1;
else
return n * this.Invoke(n - 1);
}
}
Tail Recursive Version
Here is the decompiled C# code for the optimized tail recursive version, where we can see that this has been converted into a simple for loop which is ALL contained in a single call to the Invoke() method. Which puts us in a much better/happier place.
[Serializable]
internal class tailRecursiveFactorial\u004021 : OptimizedClosures.FSharpFunc<int, int, int>
{
internal tailRecursiveFactorial\u004021()
{
}
public override int Invoke(int x, int acc)
{
for (; x > 1; {
int num;
x = num;
}
)
{
num = x - 1;
acc *= x;
}
return acc;
}
}
[Serializable]
internal class factorialProducingForLoop\u004020 : FSharpFunc<int, int>
{
internal factorialProducingForLoop\u004020()
{
}
public override int Invoke(int x)
{
return FSharpFunc<int, int>.InvokeFast<int>(
(FSharpFunc<int, FSharpFunc<int, int>>) new Program.tailRecursiveFactorial\u004021(), x, 1);
}
I just wanted to mention one more thing, if you took this already cool (and totally fit for purpose) tail recursive code:
let factorialProducingForLoop x =
// Keep track of both x and an accumulator value (acc)
let rec tailRecursiveFactorial x acc =
if x <= 1 then
acc
else
tailRecursiveFactorial (x - 1) (acc * x)
tailRecursiveFactorial x 1
Which gave us these results:
But instead decided you prefer to write it like this where we DO NOT create an inner recursive function, but rather choose to have 2 separate functions, and we alter the order of the value and the accumulator:
let rec tailRecursiveFactorial acc x =
if x <= 1 then
acc
else
tailRecursiveFactorial (acc * x) (x - 1)
let factorialProducingWhileLoop data = tailRecursiveFactorial 1 data
printfn "factorialProducingWhileLoop 5 = %A" (factorialProducingWhileLoop 5)
It can be seen we get the same results, but lets examine the decompiled code:
[Serializable]
internal class tailRecursiveFactorial\u004032 : OptimizedClosures.FSharpFunc<int, int, int>
{
internal tailRecursiveFactorial\u004032()
{
}
public override int Invoke(int acc, int x)
{
while (x > 1)
{
int num = acc * x;
--x;
acc = num;
}
return acc;
}
}
[Serializable]
internal class factorialProducingWhileLoop\u004037 : FSharpFunc<int, int>
{
public FSharpFunc<int, FSharpFunc<int, int>> tailRecursiveFactorial;
internal factorialProducingWhileLoop\u004037(FSharpFunc<int, FSharpFunc<int, int>> tailRecursiveFactorial)
{
this.tailRecursiveFactorial = tailRecursiveFactorial;
}
public override int Invoke(int data)
{
return FSharpFunc<int, int>.InvokeFast<int>(this.tailRecursiveFactorial, 1, data);
}
}
It can be seen that this time we get a while loop in the Invoke() method call.
I don’t know if this adds any value to the post, but I just wanted to see what would happen if I swapped the order and had no nested function, and instead went for 2 functions instead of one function that had an inner function.
I guess I am just a geek (and proud of it)
Callbacks
There is another way to deal with recursion which uses a callback based technique, but too be honest I have found it not to be that easy to understand, and a little hairy for right here, right now. If you are interested I am sure a quick Google around will get you what you want.
So in the end this post was quite a short one for a fairly complex subject, but there is not much more I wanted to say.






I think the second method called Continuation passing style.